一、Self-Attention
1.1. 为什么要使用Self-Attention
假设现在一有个词性标注(POS Tags)的任务，例如：输入I saw a saw（我看到了一个锯子）这句话，目标是将每个单词的词性标注出来，最终输出为N, V, DET, N(名词、动词、定冠词、名词)。
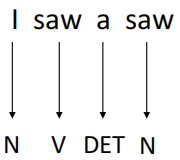
这句话中，第一个saw为动词，第二个saw(锯子)为名词。如果想做到这一点，就需要保证机器在看到一个向量(单词)时，要同时考虑其上下文，并且，要能判断出上下文中每一个元素应该考虑多少。例如，对于第一个saw，要更多的关注I，而第二个saw，就应该多关注a。
这个时候，就要Attention机制来提取这种关系：如果一个任务的输入是一个Sequence（一排向量），而且各向量之间有一定关系，那么就要利用Attention机制来提取这种关系。
1.2. 直观的感受下Self-Attention
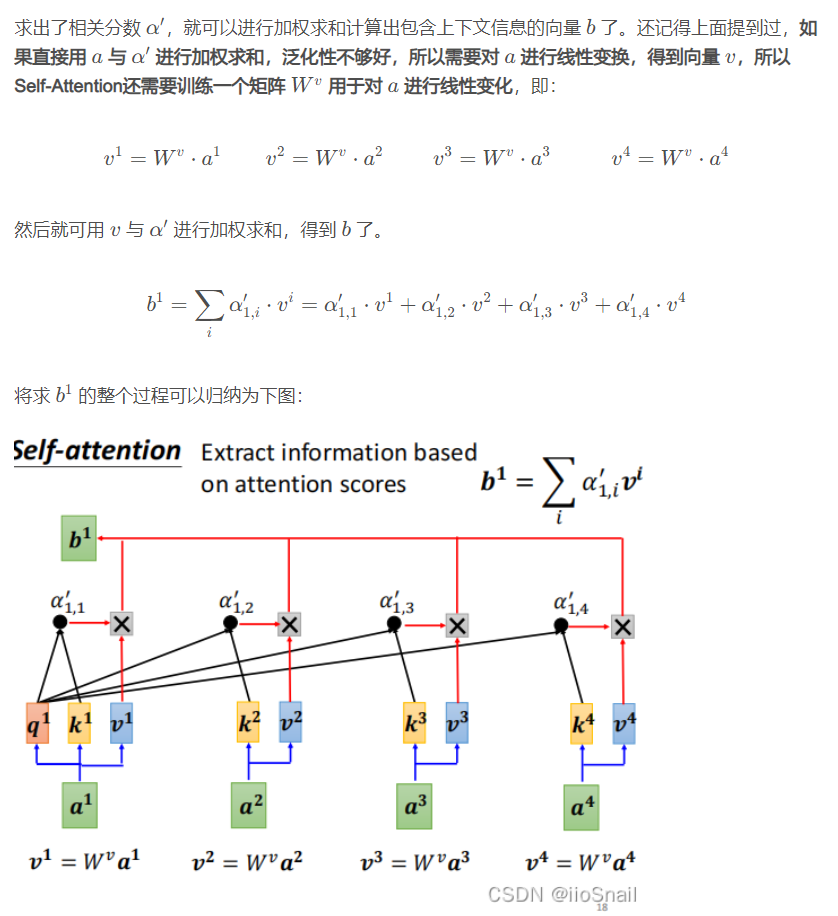
该图描述了Self-Attention的使用。Self-Attention接受一个Sequence（一排向量，可以是输入，也可以是前面隐层的输出），然后Self-Attention输出一个长度相同的Sequence，该Sequence的每个向量都充分考虑了上下文。 举个例子，输入是I、saw、a、saw，对应向量为：
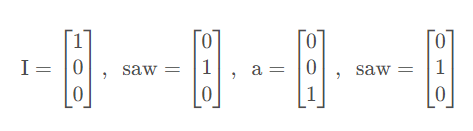
在经过Self-Attention层之后，实际上计算了Softmax就会变成了这样：
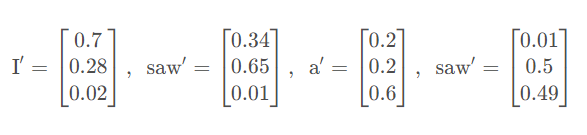
对于第一个saw，它除了自身外，还要考虑 0.34 0.340.34个I；对于第二个saw，它要考虑0.49 0.490.49个a
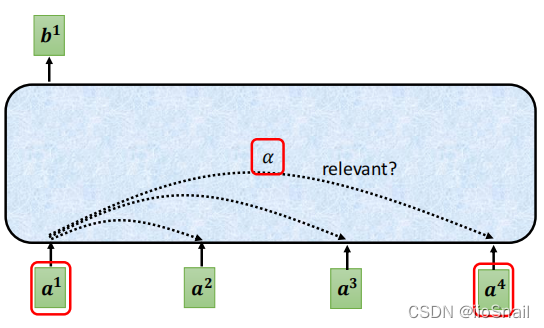
1.3. Self-Attenion是如何考虑上下文的
如图所示，每个输入都会和其他输入计算一个相关性分数，然后基于该分数，输出包含上下文信息的新向量。
同理，对于b2，也是计算权重然后进行加权求和。
如果按照上面这个式子做，还有两个问题：
- α之和不为1，这样会将输入向量放大或缩小
- 直接用输入向量去乘的话，拟合能力不够好
对于问题1，通常的做法是将α过一个Softmax（当然也可以选择其他的方式）
对于问题2，通常是将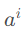
乘个矩阵(该矩阵是训练出来的)，然后生成
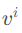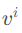，然后用去乘α。
1.4. 如何计算相关性分数 α
首先，复习下向量相乘。两个向量相乘（做内积），公式为：a ⋅ b = ∣a∣∣b∣cos θ，通过公式可以很容易得出结论：
- 两个向量夹角越小（越接近），其内积越大，相关性越高 。反之，两个向量夹角越大，相关性越差，如果夹角为90°，两向量垂直，内积为0，无相关性
通过上面的结论，很容易想到，要计算 a^1和 a^2的相关性，直接做内积即可，即
即 α_{1,2} =a1⋅a2。 但如果直接这样，显然不好，例如，句子I saw a saw的saw和saw相关性一定很高(两个一样的向量夹角为0)，这样不就错了嘛。
为了解决上面这个问题，Self-Attention又额外“训练”了两个矩阵Wq和Wk
- Wq 负责对“主角”进行线性变化，将其变换为q，称为query，
- Wk 负责对“配角”进行线性变化，将其变换为q，称为key
有了Wq和Wk，我们就可以计算 a^1和a^2的相关分数α_{1,2}，即：
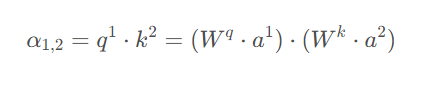
上面这些内容可以汇总成如下图：
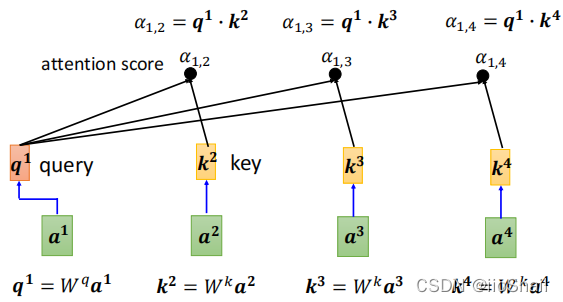
上图没有把K1画出来，但实际计算的时候，需要计算K1，即需要计算a1和其自身的相关性分类。
1.5. 将α归一化
还记得上面提到的，α之和不为1，所以，在上面得到了α{1,*}后，还需要过一下Softmax，将α进行归一化。如下图：
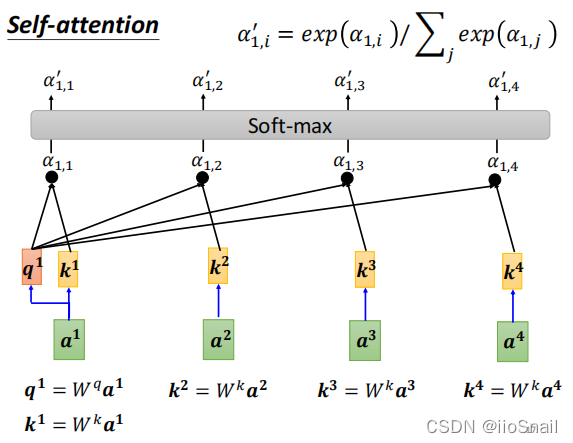
最终，会将归一化后的α'{1,*}作为a1与其他向量的相关分数，同理，a2...an向量与其他向量的相关分数也这么求。
- 不一定非要用Softmax，你开心想用什么都行，说不定效果还不错，也不一定非要归一化。 只是通常是这么做的
