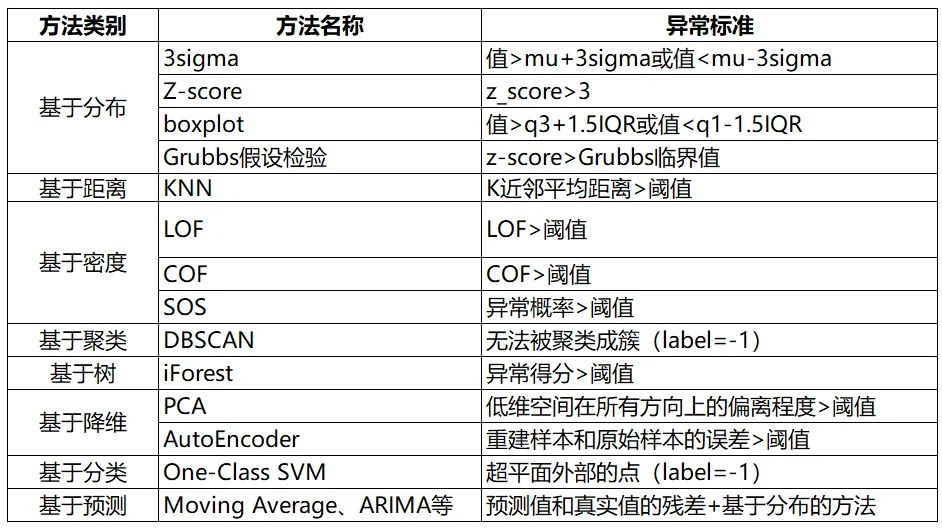
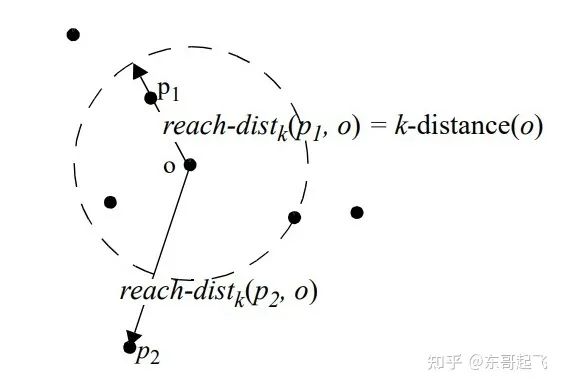
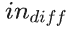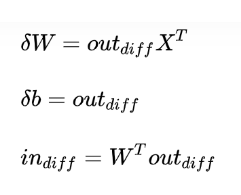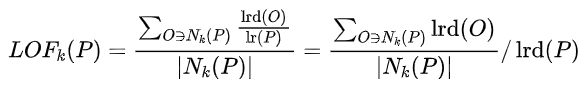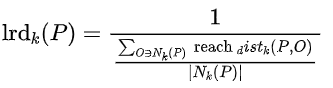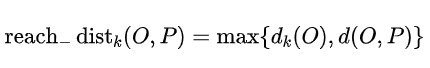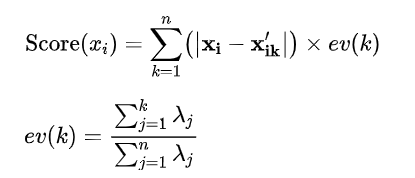情感分类实战
词表映射Vocab
from collections import defaultdict
# 词表映射
class Vocab:
def __init__(self, tokens=None):
# 索引对应token的列表
self.idx_to_token = list()
# token和索引的词典
self.token_to_idx = dict()
if tokens is not None:
# 在tokens列表后加标记<unk>来分辨未登录词
if '<unk>' not in tokens:
tokens = tokens + ['<unk>']
for token in tokens:
self.idx_to_token.append(token)
# 下标从0开始
self.token_to_idx[token] = len(self.idx_to_token) - 1
self.unk = self.token_to_idx['<unk>']
@classmethod
def build(cls, text, min_freq=1, reserved_tokens=None):
# 若查找不存在，返回0
token_freqs = defaultdict(int)
for sentence in text:
for token in sentence:
token_freqs[token] += 1
# 不重复tokens列表
uniq_tokens = ['<unk>'] + (reserved_tokens if reserved_tokens else [])
uniq_tokens += [token for token, freq in token_freqs.items() if freq >= min_freq and token != '<unk>']
return cls(uniq_tokens)
def __len__(self):
# 返回词表的大小，即此表中有多少个互不相同的标记
return len(self.idx_to_token)
def __getitem__(self, item):
# 查找输入标记对应的索引值，如果该标记不存在，则返回标记<unk>的索引值（0）
return self.token_to_idx.get(item, self.unk)
def convert_token_to_idx(self, tokens):
# 查找一系列输入标记对应的索引值
return [self.token_to_idx[token] for token in tokens]
def convert_idx_to_token(self, idxs):
# 查找一系列索引值对应的标记
return [self.idx_to_token[idx] for idx in idxs]
Embedding层
将一个词（或者标记）转换为一个低维、稠密、连续的词向量（也称Embed-ding）是一种基本的词表示方法，通过torch.nn包提供的Embedding层即可实现该功能。
创建Embedding对象时，需要提供两个参数，分别是num_embeddings，即词表的大小；以及embedding_dim，即Embedding向量的维度。
embedding = nn.Embedding(8,3) # 词表大小为8，Embedding向量维度为3
input = torch.tensor([[0,1,2,1],[4,6,6,7]], dtype=torch.long)
# 输入形状为(2,4)的整数张量（相当于两个长度为4的整数序列）
# 其中每个整数范围在0-7
output = embedding(input) #调用Embedding对象
print(output) # 输出结果，其中将相同的整数映射为相同的向量
融入词向量层的MLP
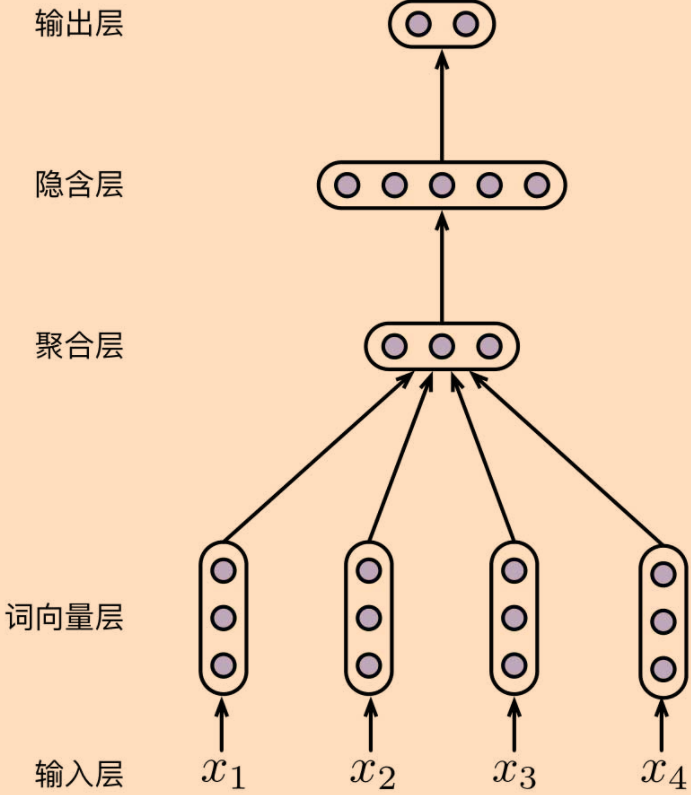
import torch
from torch import nn
from torch.nn import functional as F
class MLP(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, num_class):
super(MLP, self).__init__()
"""
词袋（Bag-Of-Words，BOW）模型解决该问题。
词袋模型指的是在表示序列时，不考虑其中元素的顺序，
而是将其简单地看成是一个集合"""
# 词嵌入层
self.embedding = nn.Embedding(vocab_size, embedding_dim)
# 线性变换：词嵌入层->隐含层
self.linear1 = nn.Linear(embedding_dim, hidden_dim)
# 使用ReLU激活函数
self.activate = F.relu
# 线性变换：激活层->输出层
self.linear2 = nn.Linear(hidden_dim, num_class)
def forward(self, inputs):
embeddings = self.embedding(inputs)
# 将序列中多个embedding进行聚合（此处是求平均值）
embedding = embeddings.mean(dim=1)
hidden = self.activate(self.linear1(embedding))
outputs = self.linear2(hidden)
# 获得每个序列属于某一类别概率的对数值
probs = F.log_softmax(outputs, dim=1)
return probs
mlp = MLP(vocab_size=8, embedding_dim=3, hidden_dim=5, num_class=2)
# 输入为两个长度为4的整数序列
inputs = torch.tensor([[0, 1, 2, 1], [4, 6, 6, 7]], dtype=torch.long)
outputs = mlp(inputs)
# 最终的输出结果为每个序列属于某一类别概率的对数值。
print(outputs)
#tensor([[-0.9175, -0.5100],
# [-0.8011, -0.5957]], grad_fn=<LogSoftmaxBackward>)
词表映射 -> 词向量层 -> 融入词向量层的多层感知器 -> 数据处理
EmbeddingBag
由于在一个batch中输入的文本长度往往是不固定的，因此无法像上面的代码一样简单地用一个张量存储词向量并求平均值。
在调用Embedding-Bag层时，首先需要将不定长的序列拼接起来，然后使用一个偏移向量Offsets记录每个序列的起始位置。举个例子，假设一个批次中有4个序列，长度分别为4、5、3和6，将这些长度值构成一个列表，并在前面加入0（第一个序列的偏移量），构成列表offsets=[0，4，5，3，6]，然后使用语句torch.tensor（offsets [：-1]）获得张量[0，4，5，3]，后面紧接着执行cumsum（dim=0）方法（累加），获得新的张量[0，4，9，12]，这就是最终每个序列起始位置的偏移向量。
import torch
import torch.nn as nn
input1 = torch.tensor([0, 1, 2, 1], dtype=torch.long)
input2 = torch.tensor([2, 1, 3, 7, 5], dtype=torch.long)
input3 = torch.tensor([6, 4, 2], dtype=torch.long)
input4 = torch.tensor([1, 3, 4, 3, 5, 7], dtype=torch.long)
inputs = [ input1, input2, input3, input4]
offsets = [0] + [i.shape[0] for i in inputs]
print (offsets)
# [0, 4, 5, 3, 6]
offsets = torch.tensor(offsets [:-1]).cumsum(dim=0)
print (offsets)
# tensor([ 0, 4, 9, 12])
inputs = torch.cat(inputs)
print (inputs)
# tensor([0, 1, 2, 1, 2, 1, 3, 7, 5, 6, 4, 2, 1, 3, 4, 3, 5, 7])
embeddingbag = nn.EmbeddingBag(num_embeddings=8, embedding_dim=3)
embeddings = embeddingbag (inputs, offsets)
print (embeddings)
# tensor([[ 0.6831, 0.7053, -0.5219],
# [ 1.3229, 0.2250, -0.8824],
# [-1.3862, -0.4153, -0.5707],
# [1.3530, 0.1803, -0.7379]], grad_fn=<EmbeddingBagBackward>)
数据处理
使用NLTK提供的sentence_polarity句子倾向性数据。
import torch
from vocab import Vocab
def load_sentence_polarity():
from nltk.corpus import sentence_polarity
vocab = Vocab.build(sentence_polarity.sents())
train_data = [(vocab.convert_tokens_to_ids(sentence), 0)
for sentence in sentence_polarity.sents(categories='pos')[:4000]] \
+ [(vocab.convert_tokens_to_ids(sentence), 1)
for sentence in sentence_polarity.sents(categories='neg')[:4000]]
test_data = [(vocab.convert_tokens_to_ids(sentence), 0)
for sentence in sentence_polarity.sents(categories='pos')[4000:]] \
+ [(vocab.convert_tokens_to_ids(sentence), 1)
for sentence in sentence_polarity.sents(categories='neg')[4000:]]
return train_data, test_data, vocab
通过以上数据处理非常的不方便，因此PyTorch提供了DataLoader类。下面我创建一个BowDataset子类继承DataLoader，其中Bow是词袋的意思。
class BowDataset(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, i):
return self.data[i]
# collate_fn参数指向一个函数，用于对一个批次的样本进行整理，如将其转换为张量等。具体代码如下。
def collate_fn(examples):
inputs = [torch.tensor(ex[0]) for ex in examples]
targets = torch.tensor([ex[1] for ex in examples], dtype=torch.long)
offsets = [0] + [i.shape[0] for i in inputs]
offsets = torch.tensor(offsets[:-1]).cumsum(dim=0)
inputs = torch.cat(inputs)
return inputs, offsets, targets
基于MLP的情感分类
import torch
from torch import nn, optim
from torch.nn import functional as F
from torch.utils.data import Dataset, DataLoader
from collections import defaultdict
from vocab import Vocab
from utils import load_sentence_polarity
class BowDataset(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, i):
return self.data[i]
def collate_fn(examples):
inputs = [torch.tensor(ex[0]) for ex in examples]
targets = torch.tensor([ex[1] for ex in examples], dtype=torch.long)
offsets = [0] + [i.shape[0] for i in inputs]
offsets = torch.tensor(offsets[:-1]).cumsum(dim=0)
inputs = torch.cat(inputs)
return inputs, offsets, targets
class MLP(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, num_class):
super(MLP, self).__init__()
self.embedding = nn.EmbeddingBag(vocab_size, embedding_dim)
self.linear1 = nn.Linear(embedding_dim, hidden_dim)
self.activate = F.relu
self.linear2 = nn.Linear(hidden_dim, num_class)
def forward(self, inputs, offsets):
embedding = self.embedding(inputs, offsets)
hidden = self.activate(self.linear1(embedding))
outputs = self.linear2(hidden)
log_probs = F.log_softmax(outputs, dim=1)
return log_probs
# tqdm是一个Python模块，能以进度条的方式显示迭代的进度
from tqdm.auto import tqdm
# 超参数设置
embedding_dim = 128
hidden_dim = 256
num_class = 2
batch_size = 32
num_epoch = 5
# 加载数据
train_data, test_data, vocab = load_sentence_polarity()
train_dataset = BowDataset(train_data)
test_dataset = BowDataset(test_data)
train_data_loader = DataLoader(train_dataset, batch_size=batch_size, collate_fn=collate_fn, shuffle=True)
test_data_loader = DataLoader(test_dataset, batch_size=1, collate_fn=collate_fn, shuffle=False)
# 加载模型
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = MLP(len(vocab), embedding_dim, hidden_dim, num_class)
model.to(device) # 将模型加载到CPU或GPU设备
#训练过程
nll_loss = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001) # 使用Adam优化器
model.train()
for epoch in range(num_epoch):
total_loss = 0
for batch in tqdm(train_data_loader, desc=f"Training Epoch {epoch}"):
inputs, offsets, targets = [x.to(device) for x in batch]
log_probs = model(inputs, offsets)
loss = nll_loss(log_probs, targets)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f"Loss: {total_loss:.2f}")
# 测试过程
acc = 0
for batch in tqdm(test_data_loader, desc=f"Testing"):
inputs, offsets, targets = [x.to(device) for x in batch]
with torch.no_grad():
output = model(inputs, offsets)
acc += (output.argmax(dim=1) == targets).sum().item()
# 输出在测试集上的准确率
print(f"Acc: {acc / len(test_data_loader):.2f}")
基于CNN的情感分类
class CnnDataset(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, i):
return self.data[i]
def collate_fn(examples):
inputs = [torch.tensor(ex[0]) for ex in examples]
targets = torch.tensor([ex[1] for ex in examples], dtype=torch.long)
# 对batch内的样本进行padding，使其具有相同长度
# pad_sequence函数实现补齐（Padding）功能，
#使得一个批次中全部序列长度相同（同最大长度序列），不足的默认使用0补齐。
inputs = pad_sequence(inputs, batch_first=True)
return inputs, targets
# 模型不同，需要从nn.Module类派生一个CNN子类
# CNN额外需要传入的参数，filter_size： 卷积核大小, num_filter：卷积核个数
class CNN(nn.Module):
def __init__(self, vocab_size, embedding_dim, filter_size, num_filter, num_class):
super(CNN, self).__init__()
self.embedding = nn.Embedding(vocab_size, embedding_dim)
self.conv1d = nn.Conv1d(embedding_dim, num_filter, filter_size, padding=1)
self.activate = F.relu
self.linear = nn.Linear(num_filter, num_class)
def forward(self, inputs):
embedding = self.embedding(inputs)
convolution = self.activate(self.conv1d(embedding.permute(0, 2, 1)))
pooling = F.max_pool1d(convolution, kernel_size=convolution.shape[2])
outputs = self.linear(pooling.squeeze(dim=2))
log_probs = F.log_softmax(outputs, dim=1)
return log_probs
#tqdm是一个Pyth模块，能以进度条的方式显示迭代的进度
from tqdm.auto import tqdm
#超参数设置
embedding_dim = 128
hidden_dim = 256
num_class = 2
batch_size = 32
num_epoch = 5
filter_size = 3
num_filter = 100
#加载数据
train_data, test_data, vocab = load_sentence_polarity()
train_dataset = CnnDataset(train_data)
test_dataset = CnnDataset(test_data)
train_data_loader = DataLoader(train_dataset, batch_size=batch_size, collate_fn=collate_fn, shuffle=True)
test_data_loader = DataLoader(test_dataset, batch_size=1, collate_fn=collate_fn, shuffle=False)
#加载模型
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = CNN(len(vocab), embedding_dim, filter_size, num_filter, num_class)
model.to(device) #将模型加载到CPU或GPU设备
#训练过程
nll_loss = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001) #使用Adam优化器
model.train()
for epoch in range(num_epoch):
total_loss = 0
for batch in tqdm(train_data_loader, desc=f"Training Epoch {epoch}"):
inputs, targets = [x.to(device) for x in batch]
log_probs = model(inputs)
loss = nll_loss(log_probs, targets)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f"Loss: {total_loss:.2f}")
#测试过程
acc = 0
for batch in tqdm(test_data_loader, desc=f"Testing"):
inputs, targets = [x.to(device) for x in batch]
with torch.no_grad():
output = model(inputs)
acc += (output.argmax(dim=1) == targets).sum().item()
#输出在测试集上的准确率
print(f"Acc: {acc / len(test_data_loader):.2f}")
基于LSTM的情感分类
class LstmDataset(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, i):
return self.data[i]
def collate_fn(examples):
lengths = torch.tensor([len(ex[0]) for ex in examples])
inputs = [torch.tensor(ex[0]) for ex in examples]
targets = torch.tensor([ex[1] for ex in examples], dtype=torch.long)
# 对batch内的样本进行padding，使其具有相同长度
inputs = pad_sequence(inputs, batch_first=True)
return inputs, lengths, targets
class LSTM(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, num_class):
super(LSTM, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim, batch_first=True)
self.output = nn.Linear(hidden_dim, num_class)
def forward(self, inputs, lengths):
embeddings = self.embeddings(inputs)
#lengths必须加载到cpu中
x_pack = pack_padded_sequence(embeddings, lengths.cpu(), batch_first=True, enforce_sorted=False)
hidden, (hn, cn) = self.lstm(x_pack)
outputs = self.output(hn[-1])
log_probs = F.log_softmax(outputs, dim=-1)
return log_probs
基于Transformer 的情感分类
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=512):
super(PositionalEncoding, self).__init__()
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0).transpose(0, 1)
# 位置编码不进行参数更新
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:x.size(0), :]
return x
class Transformer(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, num_class,
dim_feedforward=512, num_head=2, num_layers=2, dropout=0.1, max_len=128, activation: str = "relu"):
super(Transformer, self).__init__()
# 词嵌入层
self.embedding_dim = embedding_dim
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
# 位置编码层
self.position_embedding = PositionalEncoding(embedding_dim, dropout, max_len)
# 编码层：使用Transformer
encoder_layer = nn.TransformerEncoderLayer(hidden_dim, num_head, dim_feedforward, dropout, activation)
self.transformer = nn.TransformerEncoder(encoder_layer, num_layers)
# 输出层
self.output = nn.Linear(hidden_dim, num_class)
def forward(self, inputs, lengths):
inputs = torch.transpose(inputs, 0, 1)
hidden_states = self.embeddings(inputs)
hidden_states = self.position_embedding(hidden_states)
attention_mask = length_to_mask(lengths) == False
hidden_states = self.transformer(hidden_states, src_key_padding_mask=attention_mask)
hidden_states = hidden_states[0, :, :]
output = self.output(hidden_states)
log_probs = F.log_softmax(output, dim=1)
return log_probs
# 准确率为67%左右
词性标注实战
基于LSTM的词性标注
WEIGHT_INIT_RANGE = 0.1
class LstmDataset(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, i):
return self.data[i]
def collate_fn(examples):
lengths = torch.tensor([len(ex[0]) for ex in examples])
inputs = [torch.tensor(ex[0]) for ex in examples]
targets = [torch.tensor(ex[1]) for ex in examples]
inputs = pad_sequence(inputs, batch_first=True, padding_value=vocab["<pad>"])
targets = pad_sequence(targets, batch_first=True, padding_value=vocab["<pad>"])
return inputs, lengths, targets, inputs != vocab["<pad>"]
def init_weights(model):
for param in model.parameters():
torch.nn.init.uniform_(param, a=-WEIGHT_INIT_RANGE, b=WEIGHT_INIT_RANGE)
class LSTM(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, num_class):
super(LSTM, self).__init__()
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.lstm = nn.LSTM(embedding_dim, hidden_dim, batch_first=True)
self.output = nn.Linear(hidden_dim, num_class)
init_weights(self)
def forward(self, inputs, lengths):
embeddings = self.embeddings(inputs)
#这里的lengths必须载入cpu
x_pack = pack_padded_sequence(embeddings, lengths.cpu(), batch_first=True, enforce_sorted=False)
hidden, (hn, cn) = self.lstm(x_pack)
hidden, _ = pad_packed_sequence(hidden, batch_first=True)
outputs = self.output(hidden)
log_probs = F.log_softmax(outputs, dim=-1)
return log_probs
embedding_dim = 128
hidden_dim = 256
batch_size = 32
num_epoch = 5
#加载数据
train_data, test_data, vocab, pos_vocab = load_treebank()
train_dataset = LstmDataset(train_data)
test_dataset = LstmDataset(test_data)
train_data_loader = DataLoader(train_dataset, batch_size=batch_size, collate_fn=collate_fn, shuffle=True)
test_data_loader = DataLoader(test_dataset, batch_size=1, collate_fn=collate_fn, shuffle=False)
num_class = len(pos_vocab)
#加载模型
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = LSTM(len(vocab), embedding_dim, hidden_dim, num_class)
model.to(device) #将模型加载到GPU中（如果已经正确安装）
#训练过程
nll_loss = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001) #使用Adam优化器
model.train()
for epoch in range(num_epoch):
total_loss = 0
for batch in tqdm(train_data_loader, desc=f"Training Epoch {epoch}"):
inputs, lengths, targets, mask = [x.to(device) for x in batch]
log_probs = model(inputs, lengths)
loss = nll_loss(log_probs[mask], targets[mask])
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f"Loss: {total_loss:.2f}")
#测试过程
acc = 0
total = 0
for batch in tqdm(test_data_loader, desc=f"Testing"):
inputs, lengths, targets, mask = [x.to(device) for x in batch]
with torch.no_grad():
output = model(inputs, lengths)
acc += (output.argmax(dim=-1) == targets)[mask].sum().item()
total += mask.sum().item()
#输出在测试集上的准确率
print(f"Acc: {acc / total:.2f}")
#准确率0.92
基于Transformer的词性标注
from utils import load_treebank
#tqdm是一个Pyth模块，能以进度条的方式显式迭代的进度
from tqdm.auto import tqdm
class TransformerDataset(Dataset):
def __init__(self, data):
self.data = data
def __len__(self):
return len(self.data)
def __getitem__(self, i):
return self.data[i]
def collate_fn(examples):
lengths = torch.tensor([len(ex[0]) for ex in examples])
inputs = [torch.tensor(ex[0]) for ex in examples]
targets = [torch.tensor(ex[1]) for ex in examples]
# 对batch内的样本进行padding，使其具有相同长度
inputs = pad_sequence(inputs, batch_first=True, padding_value=vocab["<pad>"])
targets = pad_sequence(targets, batch_first=True, padding_value=vocab["<pad>"])
return inputs, lengths, targets, inputs != vocab["<pad>"]
class PositionalEncoding(nn.Module):
def __init__(self, d_model, dropout=0.1, max_len=512):
super(PositionalEncoding, self).__init__()
pe = torch.zeros(max_len, d_model)
position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0) / d_model))
pe[:, 0::2] = torch.sin(position * div_term)
pe[:, 1::2] = torch.cos(position * div_term)
pe = pe.unsqueeze(0).transpose(0, 1)
self.register_buffer('pe', pe)
def forward(self, x):
x = x + self.pe[:x.size(0), :]
return x
class Transformer(nn.Module):
def __init__(self, vocab_size, embedding_dim, hidden_dim, num_class,
dim_feedforward=512, num_head=2, num_layers=2, dropout=0.1, max_len=512, activation: str = "relu"):
super(Transformer, self).__init__()
# 词嵌入层
self.embedding_dim = embedding_dim
self.embeddings = nn.Embedding(vocab_size, embedding_dim)
self.position_embedding = PositionalEncoding(embedding_dim, dropout, max_len)
# 编码层：使用Transformer
encoder_layer = nn.TransformerEncoderLayer(hidden_dim, num_head, dim_feedforward, dropout, activation)
self.transformer = nn.TransformerEncoder(encoder_layer, num_layers)
# 输出层
self.output = nn.Linear(hidden_dim, num_class)
def forward(self, inputs, lengths):
inputs = torch.transpose(inputs, 0, 1)
hidden_states = self.embeddings(inputs)
hidden_states = self.position_embedding(hidden_states)
attention_mask = length_to_mask(lengths) == False
hidden_states = self.transformer(hidden_states, src_key_padding_mask=attention_mask).transpose(0, 1)
logits = self.output(hidden_states)
log_probs = F.log_softmax(logits, dim=-1)
return log_probs
embedding_dim = 128
hidden_dim = 128
batch_size = 32
num_epoch = 5
#加载数据
train_data, test_data, vocab, pos_vocab = load_treebank()
train_dataset = TransformerDataset(train_data)
test_dataset = TransformerDataset(test_data)
train_data_loader = DataLoader(train_dataset, batch_size=batch_size, collate_fn=collate_fn, shuffle=True)
test_data_loader = DataLoader(test_dataset, batch_size=1, collate_fn=collate_fn, shuffle=False)
num_class = len(pos_vocab)
#加载模型
# device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Transformer(len(vocab), embedding_dim, hidden_dim, num_class)
model#将模型加载到GPU中（如果已经正确安装）
#训练过程
nll_loss = nn.NLLLoss()
optimizer = optim.Adam(model.parameters(), lr=0.001) #使用Adam优化器
model.train()
for epoch in range(num_epoch):
total_loss = 0
for batch in tqdm(train_data_loader, desc=f"Training Epoch {epoch}"):
inputs, lengths, targets, mask = [x for x in batch]
log_probs = model(inputs, lengths)
loss = nll_loss(log_probs[mask], targets[mask])
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f"Loss: {total_loss:.2f}")
#测试过程
acc = 0
total = 0
for batch in tqdm(test_data_loader, desc=f"Testing"):
inputs, lengths, targets, mask = [x for x in batch]
with torch.no_grad():
output = model(inputs, lengths)
acc += (output.argmax(dim=-1) == targets)[mask].sum().item()
total += mask.sum().item()
#输出在测试集上的准确率
print(f"Acc: {acc / total:.2f}")
# acc:0.82
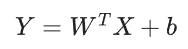
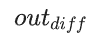，用以计算该层的梯度和输入误差
